

So before I start talking about CNNs, I would want to tell you all that I have been busy from several months and was not able to blog, but now I would try to blog at least twice in a month or may be more.
I am expecting that people who will read about this topic will have somewhat basic knowledge about Neural Networks, if not I will try my best to explain it in layman language to make it simpler to understand for almost everyone.
I have divided CNNs in to different parts as its a long topic to cover, and I will cover the rest in my another blog!
So lets start….
You might be thinking that why am I telling you about the applications of CNNs without even explaining about what it is. The reason is to motivate you all to work in this life changing field which has revolutionized the world and has had such a powerful impact.

1.CNNs are used by Google on Gmail for auto reply to the emails you receive. How it works is, CNNs goes through the whole email which you receive and suggests 3-4 best replies to you. They also use it for their photo search.
2.Facebook uses neural nets for their automatic tagging algorithms
3.Amazon for their product recommendations
4.Pinterest for their home feed personalization
5.Instagram for their search infrastructure.
I will start with what wikipedia has to say about CNNs before I give you my own perspective.
In machine learning, a convolutional neural network (CNN, or ConvNet) is a type of feed-forward artificial neural network in which the connectivity pattern between its neurons is inspired by the organization of the animal visual cortex. Individual cortical neurons respond to stimuli in a restricted region of space known as the receptive field. The receptive fields of different neurons partially overlap such that they tile the visual field. The response of an individual neuron to stimuli within its receptive field can be approximated mathematically by a convolution operation. Convolutional networks were inspired by biological processes and are variations of multilayer perceptrons designed to use minimal amounts of preprocessing.
Convolutional neural networks. Sounds like a weird combination of biology and math with a little CS sprinkled in, but these networks have been some of the most influential innovations in the field of computer vision. 2012 was the first year that neural nets grew to prominence as Alex Krizhevsky used them to win that year’s ImageNet competition (basically, the annual Olympics of computer vision), dropping the classification error record from 26% to 15%, an astounding improvement at the time.
But first, a little background. When you first heard of the term convolutional neural networks, you may have thought of something related to neuroscience or biology, and you would be right. Sort of. CNNs do take a biological inspiration from the visual cortex. The visual cortex has small regions of cells that are sensitive to specific regions of the visual field. This idea was expanded upon by a fascinating experiment by Hubel and Wiesel in 1962 (Video) where they showed that some individual neuronal cells in the brain responded (or fired) only in the presence of edges of a certain orientation. For example, some neurons fired when exposed to vertical edges and some when shown horizontal or diagonal edges. Hubel and Wiesel found out that all of these neurons were organized in a columnar architecture and that together, they were able to produce visual perception. This idea of specialized components inside of a system having specific tasks (the neuronal cells in the visual cortex looking for specific characteristics) is one that machines use as well, and is the basis behind CNNs.
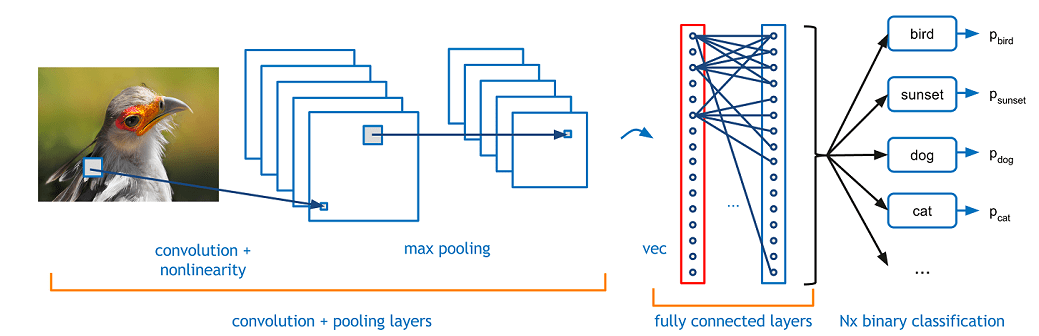
This is how a Convolutional Neural Network Looks like, you have an input image which you pass through number of convolutional layers, use activation functions on it, you do max pooling and finally comes the fully connected layers which then adds the columns and outputs the final scores of each class.
Please do not get stunned by looking at the above image and what I explained right after the image, I will explain it in much more detail later on. For now just understand the concept how humans see an image and how the computer understands it.

We all can see that the image on the left is an image which has 3 puppies, green grass. But the computer understand that image as a matrix comprising of numbers where each value represents the pixel value on that image.
To make your understanding much more clearer let me show you a Grey scale 14 x 14 image along with a 14 x 14 matrix.
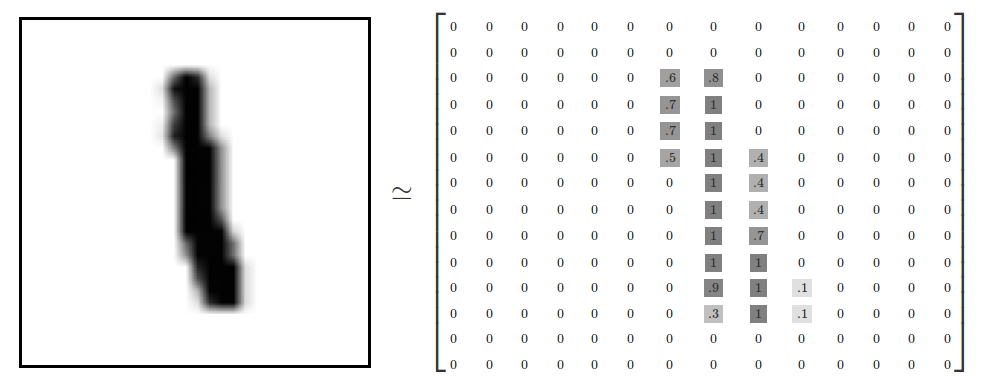
As we can see that the 14 x 14 matrix has value zero in almost every column except in columns 7,8 and 9. This is because the image on left has 1 in the center and every where else it is blank. So the matrix has some values only at that place where we can see 1 in the image on the left. I hope that helps you in understanding how we represent an image in a computer format.
When a computer sees an image (takes an image as input), it will see an array of pixel values. Depending on the resolution and size of the image, it will see a 32 x 32 x 3 array of numbers (The 3 refers to RGB values). Just to drive home the point, let’s say we have a color image in JPG form and its size is 480 x 480. The representative array will be 480 x 480 x 3. Each of these numbers is given a value from 0 to 255 which describes the pixel intensity at that point. These numbers, while meaningless to us when we perform image classification, are the only inputs available to the computer. The idea is that you give the computer this array of numbers and it will output numbers that describe the probability of the image being a certain class (.80 for cat, .15 for dog, .05 for bird, etc).
Now that we know the problem as well as the inputs and outputs, let’s think about how to approach this. What we want the computer to do is to be able to differentiate between all the images it’s given and figure out the unique features that make a dog a dog or that make a cat a cat. This is the process that goes on in our minds subconsciously as well. When we look at a picture of a dog, we can classify it as such if the picture has identifiable features such as paws or 4 legs. In a similar way, the computer is able perform image classification by looking for low level features such as edges and curves, and then building up to more abstract concepts through a series of convolutional layers. This is a general overview of what a CNN does. Let’s get into the specifics.
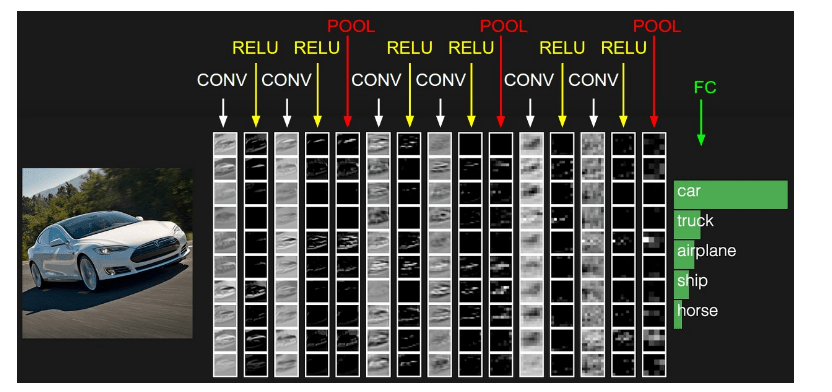
So now that I have given you enough perspective about CNNs, lets just dive deeper in to its architecture and know how it actually works. I have used this image to help you all understand CNN by picturising it in your mind as I explain you. There are lot of different images you might find on internet but I personally find this pretty intuitive in order to understand how it actually works.

We use three main types of layers to build ConvNet architectures: Convolutional Layer, Pooling Layer, and Fully-Connected Layer (exactly as seen in regular Neural Networks). We will stack these layers to form a full ConvNet architecture.
The image you see above is how CNN architecture actually looks like and I will explain you all in the same order starting from the Input till the Fully Connected layer.
1.The input is nothing but an image, for now lets just say the input is a 32 x 32 x 3 array of pixel values. 2.Now comes the first layer of CNN which is known as Convolutional Layer. CONV layer will compute the output of neurons that are connected to local regions in the input, each computing a dot product between their weights and a small region they are connected to in the input volume. This may result in volume such as [32 x 32 x 12] if we decided to use 12 filters. In order to understand Conv layer much better lets say that we have cell phone with a dimension of lets say 5*5 which covers the 5 x 5 area of a 32 x 32 image this cell phone in CNN is known as a Filter or sometimes as Neuron or Kernel and the region that it covers is called a Receptive field. This filter is also an array which consists of what we call is a Weight or Parameters (for all those who are not familiar with what weights are, for now lets assume they are just a set of randomly generated numbers in a 5 x 5 matrix). Now, let’s take the first position the filter is in for example. It would be the top left corner. As the filter is sliding, or convolving, around the input image, it is multiplying the values in the filter with the original pixel values of the image (aka computing element wise multiplications). These multiplications are all summed up (mathematically speaking, this would be 75 multiplications in total). So now you have a single number. Remember, this number is just representative of when the filter is at the top left of the image. Now, we repeat this process for every location on the input volume. (Next step would be moving the filter to the right by 1 unit, then right again by 1, and so on). Every unique location on the input volume produces a number. After sliding the filter over all the locations, you will find out that what you’re left with is a 28 x 28 x 1 array of numbers, which we call an activation map or feature map. The reason you get a 28 x 28 array is that there are 784 different locations that a 5 x 5 filter can fit on a 32 x 32 input image. These 784 numbers are mapped to a 28 x 28 array.
Let me show you with a formula how we derived a 32 x 32 x 3 array in to a 28 x 28 x 1:
(N-F)/S + 1 = (32-5)/1 + 1 = 28
N - The input array size which in this case is 32
F - Filter Size
S - The number of strides. It basically denotes how are we sliding our filter, so in this case we are sliding it in an interval of 1.
So as we can see we get 28 after subtraction, division and addition. And since we are sliding the filter once so we get an array of 28 x 28 x 1. If we would have used 12 filters instead of 1 we would have got an array of 28 x 28 x 12.
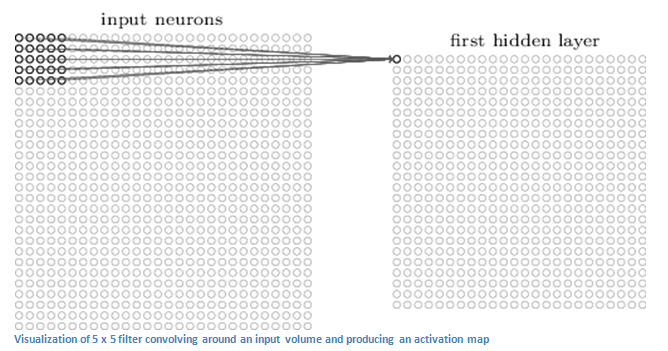
As I told you above that a filter will comprise of parameters or weights, but how do we know how many weights or parameters we require. Lets suppose we have an input image of 64 x 64 x 3 and a filter of 5 x 5 x 10, we need to find the number of parameters required which will be (5 x 5 x 3) x 10 = 750 parameters. Similarly, our new conv layer will be 60 x 60 x 10.
There is a lot to be covered in CNN, so I will cover the rest in my next blog, thanks for reading it. Hope you understood what I tried to explain. Please feel free to ask questions or any feedback you would want to give.